"If we printed out all of Jeff Bezos's money in 1 dollar bills, every day we can burn 223,104 dollars... If you re-do the calculation based on this rate, you will find that it'll take approximately 1437 years to burn all of Jeff Bezos's money..."

As of April 2020, Jeff Bezos’ net worth is 117 billion. Now, our brain is not evolved to be very good at processing big numbers, especially when the order of magnitude is in the millions or billions. This is where a little math can come in and help put things in perspective.

Let’s consider a simple problem:

Say we manage to print these 117 billion out in paper cash and start throwing them into an everlasting pit of fire that's capable of burning 1 million dollars of paper cash every day, how long would it take to burn all of Jeff Bezos's money?

A simple division can reveal a surprising answer:

$\dfrac{117 * 10 ^ 9\,\textrm{dollars}} {(1 * 10 ^ 6\,\textrm{dollars / day})} = 117 * 10 ^ 3\,\textrm{days}$

How many years is that?

$\dfrac{117 * 10^3 \,\textrm{days}}{(365 \,\textrm{days / year})} = 320 \,\textrm{years}$

Take a moment to think about that. Even if Jeff Bezos stops everything he is doing right now and just sits on his ass for the rest of his life, it will take more than 3 centuries to physically burn all of his money at the burn rate of 1 million dollars per day.

Wait a minute, is it even possible to burn 1 million dollars a day?

Well, there are 86400 seconds in a day, which means that in order to burn 1 million dollars a day, you'd have to burn at the rate:

$\dfrac{(1 * 10^6 \,\textrm{dollar / day} ) }{ (86400\,\textrm{seconds / day})} = 11.574 \,\textrm{dollars / second}$

Surprisingly (or perhaps unsurprisingly), I couldn't find any papers on how fast paper burns...

Maybe you can find out by burning some dollar bills yourself but note that burning money is illegal in some countries. Please let me know the result if you actually decide to burn real dollars.

But if we assume that paper burns more or less like wood, the most common 36-inch open fireplace can burn four 16-inch long logs per hour.¹ Let's find out how much mass of wood can be burned per hour.

$\textrm{total mass burned per hour} = \textrm{4 logs * mass (per log)} \\ mass = volume * density$

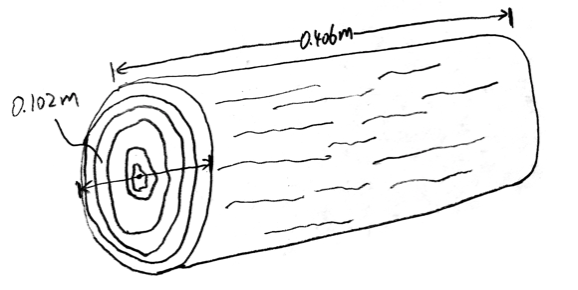
The average 16-inch long ($\approx$0.406 meters) log has a diameter of 4 inches ($\approx$0.102 meters).² Therefore, the average volume for each 16 inch log (assuming a cylinder shape) is:

$\textrm{volume} = \textrm{base\,area * length} = \pi * (\dfrac{\textrm{diameter}}{2})^2 * \textrm{length} = \pi * (\dfrac{0.102\,\textrm{m}}{2})^2 * 0.406\,\textrm{m} \approx 0.00332 \, \textrm{m}^3$

Oak trees usually have a density of 700 kg/m³; therefore, we have both pieces to get the mass of each log:

$mass = volume * density = 2.324 kg\\$

Now we just multiply by 4, since the fireplace can burn 4 logs per hour, to get our final answer:

$∴ \,\textrm{total mass burned per hour} = \textrm{4 logs * volume * density} = 4 * 0.00332 \,\textrm{m}^3 * 700 \,\textrm{kg/m}^3 = 9.296 \,\textrm{kg}$

According to the Bureau of Engraving and Printing, all U.S. bills weigh the same: 1 g. So roughly, if paper burn like wood, 9,296 dollar bills can be burned per hour, or 223,104 dollar bills per day. So how much money can we burn each day with a common fireplace after all?

• If we printed out all 5 dollar bills, every day we can burn 5 * 223104 = 1,115,520 dollars (a little more than 1 million dollars)
• If we printed out all 1 dollar bills, every day we can only burn 1 * 223104 = 223,104 dollars ($\approx$ 22.3% of 1 million dollars). If you re-do the calculation based on this rate, you will that find it'll take approximately 1437 years to burn all of Jeff Bezos's money.

The estimation could be quite different depending on how fast paper actually burns (vs. wood) and what type of fireplace is used, but the point is:

• Imagine waking up in the morning, 12 dollars are being taken out of your pocket every second ($\approx$1 million dollars in total every day). Painful, right? If you're an average American (with a net worth of $97,300), you will be completely broke before noon the very same day. In contrast, you can do this to Jeff Bezos for centuries and he will still be a billionaire.

Now, the calculation above was based on the assumption that Jeff Bezos doesn't have any income from now on; however, even if he doesn’t work, his money still earns compound interest just sitting in the bank. In fact, I will now show that even at 1% annual interest rate³, after 100 years of burning 1 million dollars a day, he will still come out to be much richer than he is now (in nominal value at least) due to the compound interest.

Let's see how Jeff Bezos's money grows over time. At the beginning of each year t, we take 365 million dollars away from the pile of Jeff Bezos's total money (whatever that amount may be at time t), the rest of it we put in a savings account to earn annual interest rate of 1%. To make the math cleaner, we define a few variables:

$I = interest \,rate = 0.01 \\ R_t = money \,Jeff\,Bezos\,has\,at\,the \,end \,of \,year\, t \\ P = R_0 = principal\, (initial\,networth) = 117 * 10^9\,(Jeff\,Bezos's\,117\,billion)\\ B = money\,burned\, each \,year = 365 * 10^6 \,(since\,we\,burn\,1\,million\,dollars\,a\,day)$

At at the end of year t, Jeff Bezos will have have:

$R_t = (1+I)(R_{t-1} - B)$

If you expand out the R_t for the first few years:

$R_2 = (1+I)(R_1-B) = (1+I)^2(P-B)-(1+I)B \\ R_3 = (1+I)(R_2-B) = (1+I)^3(P-B)-(1+I)^2B - (1+I)B\\ R_4 = (1+I)(R_3-B) = (1+I)^4(P-B)-(1+I)^3B - (1+I)^2B- (1+I) B\\ ...\\ R_n = (1+I)^n(P-B) - (1+I)^{n-1}B - (1+I)^{n-2}B - (1+I)^{n-3}B - ... - (1+I)B$

You will notice that from the second term on, Rn comes out beautifully to be a geometric series where:

$a = -(1+I)^{n-1}B\\ r = (1+I)^{-1}$

So Rn can be rewritten as the first term plus the sum of the geometric series:

$R_n = (1+I)^n(P-B) + S_m \,\,\,\,\,\,\,where\,\,m = n-1$

If we burn Jeff Bezos' money for 100 years (n = 100), he will have left:

$R_{100} = (1+I)^{100}(P-B) + S_{99}$

Where S₉₉ is the sum of the 99 terms of the geometric series:

$S_{m} = \dfrac{a(1-r^{m})}{(1-r)}$

Plugging in the terms, we get:

$S_{99} = \dfrac{-(1+I)^{n-1}B(1-(1+I)^{-99})}{(1-(1+I)^{-1})} \approx -61.86 * 10^9 \\ R_{100} = (1+I)^{100}(P-B) + S_{99} \approx 254 * 10^9 \\$

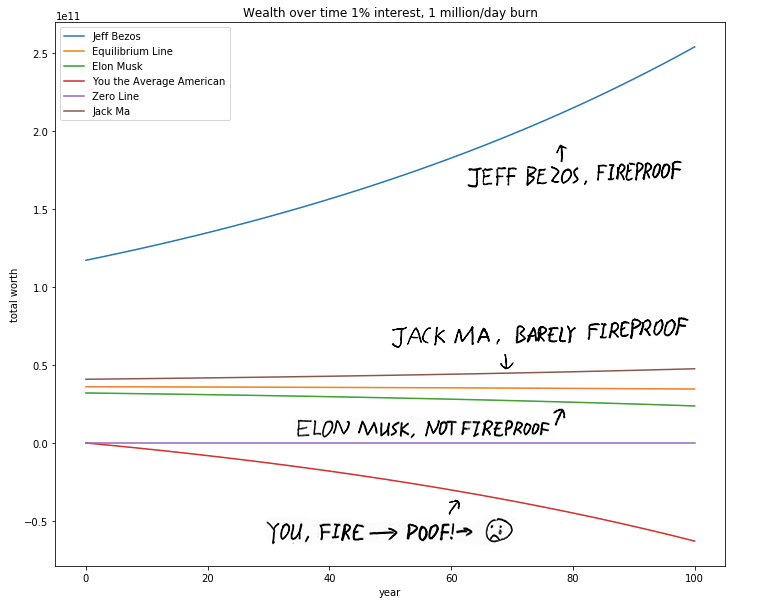
At the end of 100 years of burning, Jeff Bezos will end up 254 - 171 = 83 billions richer than he is today; this is because his initial capital is so big that the rate at which interest is earned in the bank is FASTER than the rate at which money is burned (365 million dollars a year). The natural question to ask then is how much capital do you need to have to be "fireproof" like Jeff Bezos?

This should be easy enough to get:

$P * I >= 365 * 10^6 \, dollars$

This is because the interest earned in the first year must be more than the money burned (365 million dollars); in other words, the net income must be positive for the first year. Only then, will the total pile of money you have grow, and with it, the pile of money that can be put in the bank (to earn interest), which will grow the total pile even bigger for the following year, repeating the positive cycle.

Otherwise, if the net income is negative in the first year, the total pile of money shrinks, and with in, the pile that sits in the bank for the next year and the following etc.

There is a equilibirium point (plotted in the chart below) where your total amount of wealth stays constant because your net income (interest - 365 million) is exactly 0. In this case, your total wealth will stay constant forever (in nominal value).

At I = 1%,

$P >= \dfrac{365 * 10^6}{0.01}\\ P >= 36.5 * 10^9$

You will have to have more than 36.5 billions of dollars to be fireproof!

At the time of writing, only 21 people in the world are fireproof, with the cutoff at Jack Ma (40.8 billions). Iron man Elon Musk, with his networth of 32 billions, unfortuantely is still not fireproof. See the level of wealth explained in the chart below:

Footnotes

1. The burn rate is according to eFireplaceStore.
2. According to a guide by SFGATE, "the average diameter of logs or split wood is 3 to 6 inches." We take 4 inches for the calculation.
3. Most banks state the APY (annual percentage yield) as the interest rate for savings accounts, which takes into account the effects of intra-year compounding (usually monthly, semi-quarterly or quarterly). This is different from APR (annual percentage rate). The difference is quite important if you're looking to take out loans or open a savings account, so I'd suggest research. But just remember that APY is the annual interest rate you actually get in effect.